Assignment_2

N-Queens

Gecode 6.3.0

n	Alldifferent GC		Decomposition
	fails	Time	Fails	Time
28	78,847	1s 64msec	417,027	3s 685msec
29	31,294	440msec	212,257	2s 6msec
30	1,588,827	19s 698msec	7,472,978	1m 3s

Poster Placement

Gecode 6.3.0

Instance	Naive Model		Global Model		Global+Cumulative Implied
	fails	Time	Fails	Time	Fails	Time
19x19	2,439,842	20s 734msec	300,657	2s 80msec	7,237	254msec
20x20	2,504,120	32s 604msec	2,032	74msec	943	195msec

1. Comment briefly on how the solver performance changes from one (decomposed or non-global) model to the global model, along with a justification. We can notice an improvement in both failed attempts and time elapsed for the solving time. This is due to how Global constraints functions exploit the recurring combinatorial substructures present in the problem, as global constraints, in informal terms, are common and known techniques that use specialized propagation to boost performance. The specialized propagation removes inconsistent values in the domains of our decision variables based on a specific constraint, which reduces fails as we’re cutting out the values that would lead us to a fail. Unlike decompositions, global constraints use incremental computation, which exploits cached data from past propagation algorithm calls to improve efficiency, in particular by reducing the order of complexity compared to the decomposition approach. As a result, a lower order of complexity $O$ in the propagation compared to the naive model improves time elapsed in the model.

2. BONUS Is the Cumulative resource constraint an implied constraint? why? The Cumulative Resource constraint proves to be helpful to the model as an implied constraint, as:

   • The first constraint declares that “each rectangle must fit inside the paper”, which is satisfied by the cumulative resource constraint as we have the size of the papers as capacities and time limits respectively, which pose the same spatial limits;
   • The second constraint declares that “each rectangle must not overlap”, which is satisfied since no element in the cumulative resource constraint can occupy the same position in time or the same resource as another one.

---

Prof Notes

• It would be enough to explain how the poster placement problem can be seen as a scheduling problem (as I also said before). 
  • The table’s X and Y coordinates can be seen as Time and space in the scheduling problem, since each task can be seen as a rectangle with dimensions (x,y) → (time needed, resources required)
• “The second constraint declares that “each rectangle must not overlap”, which is satisfied since no element in the cumulative resource constraint can occupy the same position in time or the same resource as another one.” → you are trying to show that no overlap is implied from the cumulative constraints (while you need to do the opposite)
  • The cumulative constraint does not work for the overlap constraint because the cumulative constraint makes sure that the sum of the resources axis is less than the max available resources, which makes it so when we represent the rectangles, they do not need to preserve the shape they’re initially given, example: 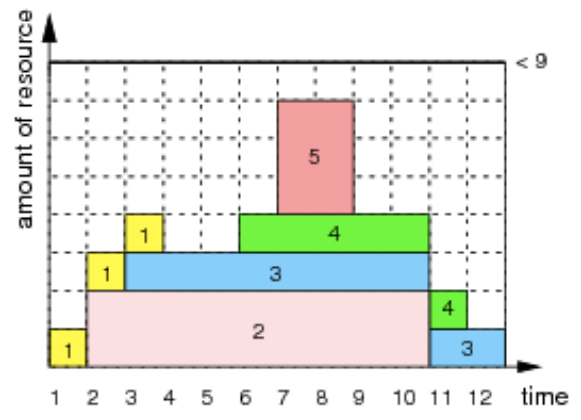the 3x1 yellow rectangle is “broken apart” in different resource heights, while we can’t do that in our poster placement problem, thus no overlap is not implied by the cumulative constraint.
• ” no element in the cumulative resource constraint can occupy the same position in time or the same resource as another one.” → why not? Two tasks can run in parallel in the same resource.
  • what i meant with this statement is that each task cannot be in the same point in time utilizing the same resource as another task, eg. (from the pic)
  • Task 2 cannot use the resource that Task 1 is using (it will use other resources in that tic of time, but not the one assigned to Task 1). This is what i meant for the no overlap argument, but i see that it’s wrong for it does not care to maintain the shape of the rectangles across the time axis.

The Sequence Puzzle

Gecode 6.3.0

n	Base		Base + Impled		Global		Global + Implied
	fails	Time	Fails	Time	Fails	Time	Fails	Time
500	652	19s 514msec	495	11s 667msec	989	248msec	493	147msec
1,000	1,362	2m 7s	995	1m 40s	1989	820msec	993	362msec

1. Going from Base → Global, and going from Base + Implied → Global + Implied: what is the main advantage of using a global constraint? Why? The main advantage is in time elapsed. This is achieved by reducing the number of variables and constraints the solver must handle, specifically:
   • In the base model we have forall(i in 0..n-1)(x[i] = sum(j in 0..n-1)(x[j] = i)), which is a meta-constraint that
     • Introduces a boolean auxiliary variable for each value compared by the x[j] = i boolean expression that resulted in a true evaluation, creating m boolean values (where m is the amount of true evaluations across all j values for that i, as i am assuming we’re not keeping the 0s);
     • Introduces m auxiliary constraints x[i] = [...] as one is generated for each boolean evaluated as true;
     • Introduces, in total, m auxiliary boolean variables, and m auxiliary constraints.
   • In the global model we have
     • only the n variables in the array x are directly involved.
     • there’s just 1 constraint which is the global one, optimized for cardinality checks. All of this is on top of the narrowed search space that the global model provides.
2. Is there an implied constraint that now becomes redundant in the Global + Implied model? Why? Yes, the constraint sum(x) = n is now redundant, here’s why: The GCC function is given the counts array, that determines the distribution of values. In our case, counts = x, making x the frequency table for x. Thus enforcing that the sum of all frequencies $x[0]+x[1]+\cdots +x[n-1]$ must equal the size of the array x. In other words, it is enforcing that $\sum _{i\in \mathrm{0..}n-1}x[i]=\text{size}(x)=n$ This makes it so the sum(x) = n is already respected as GCC ensures that the frequency counts in x are consistent with the array of size $n$.

---

Prof notes

• Q1: Your analysis does not link m and n. You should describe the numbers in terms of n, so that you can compare it the global model (which uses n variables and 1 constraint).
  • n variables are the base variables we declare in the model, while m are the aux defined ones, which makes the total variables used n+m in the base model.
  • I did not specify this as i assumed the question cared only about auxiliary variables and constraints. The actual numbers liked are
  • n+m variables (n defined, m auxiliaries), c+m constraints (c defined constraints, m aux constraints) for the base model
  • n variables and 1 constraint for the global model.