Sunti per ripasso (ITA)

Muoio :)

0 - Graphic Systems

Graphic system = Device Hardware (risorse) + software grafico (management delle risorse) per produrre immagini

device RASTER → schermi, stampanti, qualsiasi cosa sia in grado di rasterizzare in pixel

Immagini definite “Raster” (in pixel) o “Vector” (in istruzioni e dati)

Frame buffer (FB) → RAM per tenere un immagine prima di realizzarla, tiene un piano di colori

Rendering pipeline

• Geometry stage
  1. ModelView Transform → oggetti trasformati in un sistema di coordinate comune
  2. Lighting → processa il colore in base alla luce
  3. Perspective transform → ogni triangolo proiettato in un piano visivo virtuale
• Rasterization stage
  1. Fragment generation (rasterization) → triangoli visibili sono mappati in pixel
  2. Fragment processing → colori ai frammenti e geometria dalle texture per illusione dei dettagli
  3. Z-Buffer visibility test → depth buffer per nascondere pixel non visibili

1 - Modelling

1.1 - Geometry for CG

Tutto e’ basato su primitive: punti, linee, segmenti, piani, poligoni

Scalar → Magnitude (grandezza/lunghezza) Point → Location nello spazio Vector → Magnitude e direzione

Linear space

Abbiamo vettori e scalari, le operazioni tra vettori funzionano come di norma

2-norm/Euclidean norm $||a|{|}_2$ → come ricaviamo la lunghezza del vettore (basically 3D teorema di Pitagora)

Unit vector → vettore di lunghezza 1.0, un vettore puo’ essere normalizzato e diventare unit vector (o versore)

Dot product $a\cdot b=||a||||b||\cos \theta$ → ci da’ info sulla relazione dei 2 vettori (angolo tra i due)

Cross product → risulta un vettore perpendicolare ai due nell’operazione, magnitude = risultato dot product

Affine space

Spazio lineare esteso per includere i punti (e quindi coordinate)

Operazioni nuove:

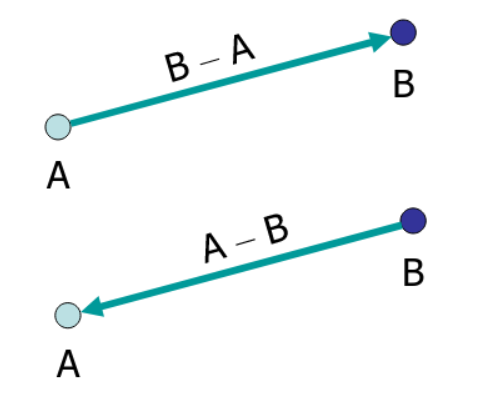
• point+vector = new point
• point-point = vector

Affine combination of a point P → combinazione lineare di punti che sommano ad 1 con i coefficienti (barycentric coordinates of P)

• Se i coefficienti $\in [0,1]$ si chiamano convex combinations
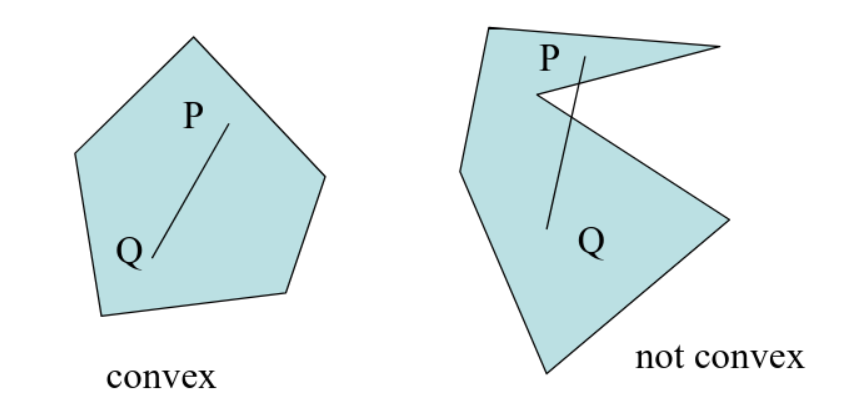
• Convex hull → set di punti che possono essere rappresentati come convex combinations

Un oggetto e’ convesso sse non puoi tracciare una linea tra 2 punti dentro l’oggetto che passa fuori l’oggetto

Barycentric coordinates → un punto definito relativamente a 3 punti definiti $P=\alpha A+\beta B+\gamma C$ $\alpha ,\beta ,\gamma$ sono le barycentric coordinates di P rispetto a A,B,C. Questo e’ importante nel warping

Piano in spazio 3D

piano $\pi$ ha una normale $n$ ed un punto d’origine, un punto appartiene sse il dot product tra il punto meno il punto d’origine ed $n$ e’ 0

Coordinate frame (Sistemi di riferimento) → quadrupla $F=(P_0,v_1,v_2,v_3)$ dove $P_0$ e’ un punto d’origine e $v_{\mathrm{1..3}}$ e’ una base vettoriale

Homogeneous coordinates → sistema di coordinate che rappresenta unicamente punti e vettori Vector $w=a_1{v}_1+a_2{v}_2+a_3{v}_3$ Point $P=P_0+a_1{v}_1+a_2{v}_2+a_3{v}_3$ defined by 4 coordinates: $[a_1,a_2,a_3,0or1]$ 0 → vector, 1 → point

Geometric Transformations

Affine transformations → vogliamo trasformare le coordinate per modificare la geometria ma non la topologia

• Position
• Orientation
• Size
• Shear Un sacco di matrici. operazioni 3D sono in matrici 4x4 invece che 3x3

1.2 - Intro to Geometric Modeling

Un oggetto puo’ essere rappresentato

• Implicitamente (come funzione)
  • facile rappresentare cose semplici
  • si gestisce facilmente matematicamente
• Esplicitamente (con un parametro) (x,y)
  • per cose piu’ complesse
• Discreto (rappresentazione grafica)

Curves and surfaces

Implicit Surface: $\varphi (x,y,z)=0$ definisce la superficie

• Function form of curves only works when each x has one y Parametric Surface: $S(u,v)=(x(u,v),y(u,v),z(u,v))$
• Parametric Form of curves works for more complex shapes (like circles).

Calcoliamo le tangenti e poi normali in un punto del piano per sapere qual e’ la parte esterna dei piani (usata nel lighting)

Continuity

$C^0$ → curve e superfici senza buchi, segmentate $C^1$ → con derivate continue, superfici lisce $C^2$ → derivate seconde continue

$G^0=C^0$ → Position continuity $G^1$ → Tangent continuity $G^2$ → Curvature continuity

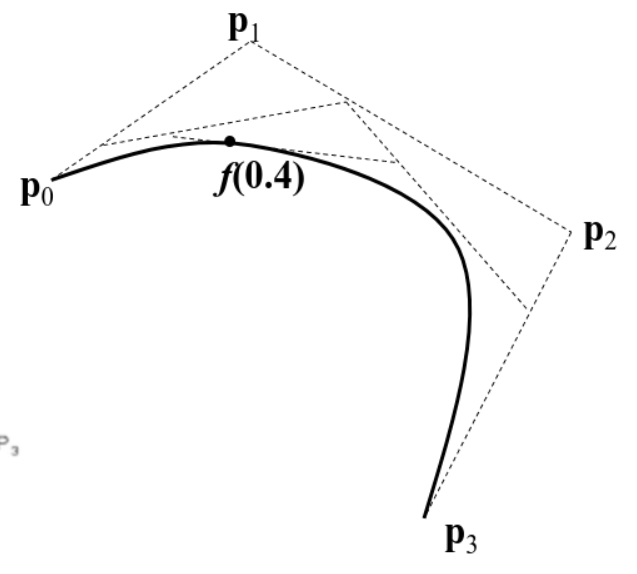
1.3 - Bézier Curves

Interpolazione → curva che deve passare nei punti di controllo Approssimazione → curva influenzata dai punti di controllo

La curva di Bézier e’ una curva che interpola dei punti di controllo (insieme punti di controllo = poligono di controllo) il grado (degree) della curva e’ uguale ai punti+1

Representing the curve

3 modi per rappresentare la curva

• Con la Bernstein Polynomial basis
• Con una polynomial in Matrix Form (sempre basato sul Bernstein basis)
  • 
• De Casteljau Algorithm (usa linear interpolation, Lerp)

Proprieta’ curva di Bézier

1. Muovere i punti di controllo modifica la curva
2. La curva interpola solo il primo ed ultimo punto di controllo
3. Ha non piu’ intersezioni con una linea che con il poligono di controllo
4. E’ invariante sotto le affine transformation (translation, rotation, scaling, shear)
5. La curva e’ smooth con derivate smooth
6. La curva e’ tangente al primo ed all’ultimo punto di controllo ed ai primi ed ultimi segmenti
7. La curva e’ contenuta nel convex hull del punto di controllo (il poligono piu’ piccolo formato dai punti di controllo)
8. Precisione lineare → quando tutti i control point formano una linea, la curva di Bézier e’ la linea di segmento che interpola tutti i punti

Linear Interpolation (Lerp) → computa un valore inbetween su base $t$ L’algoritmo De Casteljau interpola $N$ volte i punti cosi’ da arrivare ad una curva

Disegnare la curva

• Metodo uniforme → discretizza l’intervallo parametrico in $N$ punti equidistanti e unisci i punti trovati
• Metodo Suddivisione Adattuva → rompi la curva continua trovata in sottocurve abbastanza piccole e renderizza

Continuity

$C^0=G^0$ → continua, un joint puo’ essere sharp

• $C^1$ → la derivata di ogni punto e’ continua $G^1$ → Geometry Continuity, le tangenti hanno la stessa direzione $G^2$ → tangenti hanno stessa direzione e curvatura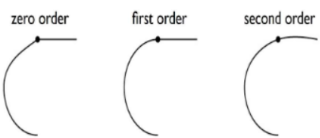
• 

1.4 Interpolazione

Interpolazione → curva che deve passare nei punti di controllo

Teorema di interpolazione dei polinomi → esiste sempre ed e’ unico un polinomio di grado n che passa per n+1 punti (soddisfa la condizione di interpolazione)

Piecewise polynomial INTERPOLATION → controllare la continuita’ della curva per manipolare l’output finale (per fare cose come la palla che rimbalza)

Catmull-Rom spline → curva di bezier costruita espandendo ogni punto con due punti aggiuntivi (+ e - per far in modo che la curva passi per il punto)

• I punti vengono calcolati approssimando la derivata di ogni punto in base al punto successivo e precedente $m_i=\frac{P_{i+1}-P_{i-1}}{2}$
• 1/3 di $m$ viene aggiunta/sottartta al punto per ricavare i punti 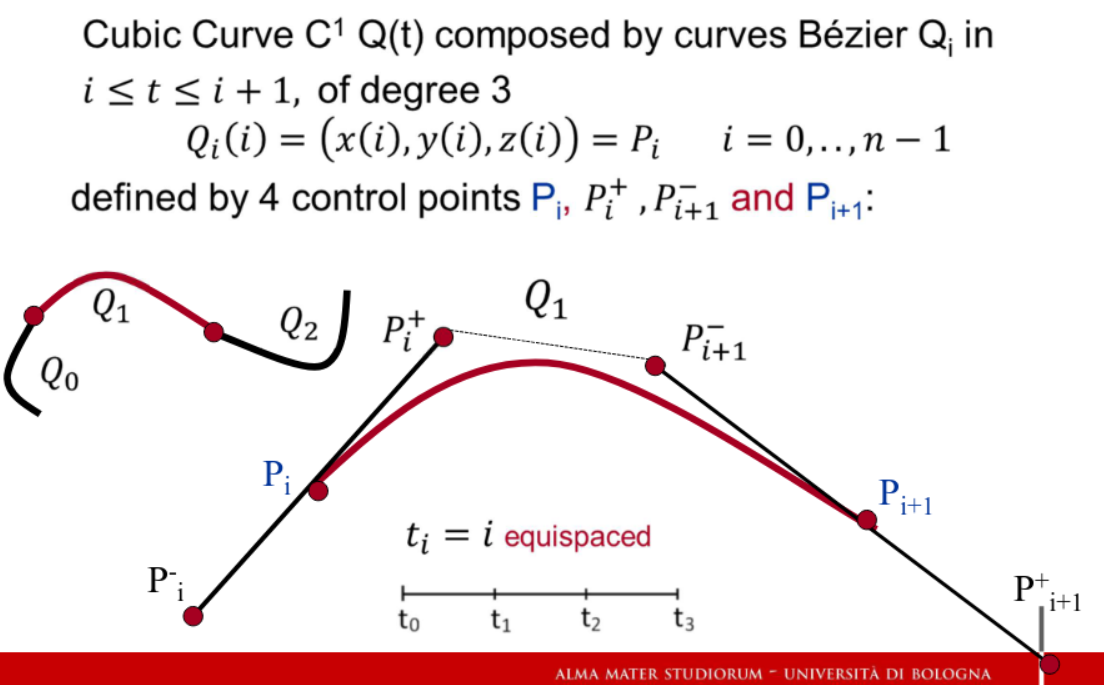TensionContinuityBias (TCB-spline) →Introduce altri parametri per la forma della curva
• tensione
• continuita’
• bias Con questi parametri computa i punti Catmull-Rom ridefiniti che danno definizione alla curva

1.5 Mesh

Mesh poligonale

Mesh poligonare → set di edge, vertici e facce connesse in modo che

• ogni edge e’ condiviso al massimo da due facce adiacenti
• una parte connette due vertici
• le facce sono sequenze di parti chiuse
• un vertex e’ condiviso da almeno due parti

Height field → file che detiene l’elevazione di un piano, di solito in un’immagine monocromatica

3 modi per generare mesh Triangulation or tetraedralization → mesh dai punti Tessellation → mesh dalle superfici Polygonalization → mesh da volumi di dati

le mesh triangolari hanno una componente geometrica (coordinate vertici) e topologica (grafo vertices, edges, faces)

Le normali delle facce e dei vertici le calcoliamo con il metodo max-nelson

Una mesh puo’ essere

• Strutturata (regolare) → numero elementi intorno ai vertici costante
• Semi-regolare → regolare tranne poche eccezioni
• Irregolare

i file .obj racchiudono mesh, sono formati che possono contenere

• lista vertici ordinati
• lista poligoni
• normali dei vertici
• coordinate texture
• facce L’orientazione delle facce e’ dato dall’ordine dei vertici (ordine antiorario)

Manifold

n-Manifolds → superficie liscia che i mesh approssimano, ogni punto ha una neighbourhood che puo’ creare un disco (per un 2D manifold)

una mesh e’ 2-manifold se i vertex interni sono homoeomorfici ad un disco e i vertex al limite homoeomorfici a mezzo disco

Discrete Laplacian $L$ (matrix) → grafo di connettivita’ delle mesh, rappresenta una mesh e contiene i pesi degli archi Normalized discrete Laplacian → normalizza i pesi

Continuous/discrete Laplace-Beltrami operator → misura la differenza tra un vertice e l’average dei vicini L’operatore e’ usato per approssimare le mesh mantenendo la topologia

Curvature → Attraverso le tangenti in un punto P di una superficie e una direzione $e_{\theta }$ dal punto P (intorno) possiamo capire la curvatura della superficie

• Possiamo calcolarci la curvatura media intorno ad un punto
• Possiamo calcolarci la curvatura gaussiana che ci dice se la curvatura e’ concava o convessa

Surface Genus → numero di curve semplici chiuse che possono essere disegnate da una superficie senza dividerle in due diverse parti connesse, aka “buchi” in una superficie orientata

Euler’s formula per una mesh chiusa → mette in relazione il numero di faces, edges e vertices in una mesh non strutturata, chiusa e connessa

• Senza boundaries → $X=|V|-|E|+|T|=2(1-g)$ (g=Genus)
• Con boundaries → boundaries $B$ $X=|V|-|E|+|T|+|B|=2(1-g)$ $X$ → euler characteristic, il numero ci da’ informazioni (eg. $X=2$, la figura e’ un cubo (???))

Geometry Mesh Processing

Operazioni per creare una mesh

1. Reconstruction
2. Simplification
   • Ottimizziamo la mesh tramite decimazione vertex e decimazione incrementale per alleggerire la mesh (basandoci sull’approssimazione dell’errore)
3. Parametization / UV MApping
   • mappare la superficie ad un dominio di parametri
   • Teorema Egregium (C. F. Gauß) → “Una superficie non puo’ essere parametrizzata senza distorsione.”
   • Lo stretch che il texture mapping soffre puo’ essere minimizzato
   • Atlas Texture generation → dividiamo il modello in pezzi per texturizzarlo
4. Remeshing
   • Distribuire i punti sulla superficie
5. Smoothing/Fairing (diminuire la variazione in una curva)
   • l’equivalente di image deniosing ma per le mesh
   • Approssimazione/smoothness
6. Deformation/Editing
7. Text-to-3D
   • Genera un modello 3D da parole
8. Shape analysis
   • Detection di simmetria, corrispondenza, segmentazione etc. (features)

2 - Rendering

2.1 Rendering Pipeline

Rendering → processo che crea immagini da scene 3D

• Pipeline-based → per ogni pixel, per ogni oggetto
• Ray-tracing → per ogni oggetto, per ogni pixel

Geometry Stage → operazioni geometriche per ogni vertex, cose come muovere oggetti, camera, clipping, proiezione, mapping a finestra

Rasterizer Stage → output geometrico diventa pixel visibili sul frame buffer (lo schermo), cose come scan conversion, interpolation, colour combining, visibility

Geometry Stage

Diversi sistemi di coordinate

• OCS - Coordinate locali di un oggetto
• WCS - World coordinates
• VCS - Coordinate telecamera
• NDC - Coordinate normalizzate per il dispositivo (Clip space)
• SCS - Screen space

View transformation

modello “look at” (Camera)

• C point → viewpoint
• A point → direzione della visione
• FOV
• Depth of field Camera in WCS = $F(C,u,v,w)$
• C → posizione
• w-axis → direzione vista
• VUP → up vector (punta in alto per la camera)

Projection transformation

Da vertici 3D in VCS a coordinate 2D, vertici visibili nello schermo Questa fase definisce la prospettiva

• Projection
  • Le linee convergono al centro della proiezione
  • Oggetti lontani appaiono piu’ piccoli
  • effetto forshortening
  • Angoli preservati solo in piani paralleli
  • realistico
  • Forma del volume di visione: piramide troncata
• Orthographic
  • Centro di proiezione locato ad infinito
  • Forma del volume di visione: cuboide troncato

Canonical view volume/Clip Space → coordinate 3D rispetto alla camera normalizzate da -1 a +1 per tutti e 3 gli assi (Vengono definite matrici per convertire le proiezioni)

Window transformation → lasciamo stare la coordinata z mentre mappiamo il resto all’immagine 2D

Clipping

la camera adatta/taglia gli oggetti che sono parzialmente fuori dal range di visione

Cohen-Sutherland Line Clipping in 2D → metodo per capire se c’e’ possibilmente bisogno di clippare un oggetto (9 regioni con al centro lo schermo, vedi le regioni di ogni punto e clippa usando l’intersezione)

E’ possibile dover aumentare i punti in un poligono clippato

Rasterization stage

Fragment generation / Rasterization

Genera frammenti (oggetti discreti a schermo) con informazioni (colore, texture)

Diversi modi per rasterizzare, abbiamo visto come rasterizzare una linea con

• Digital Differential Analyzer → per ogni x plotta una y, inverso se la linea e’ steep
• Midpoint Algorithm → prendi il pixel piu’ vicino al punto della linea
• Bresenham’s Algorithm → decidi il pixel in base al punto medio dell’edge del pixel attraversato

Rasterizziamo triangoli come segmenti di linee + identificando l’interno del triangolo (parte sinistra di ogni boundary line, dato che ordiniamo in antiorario, solo per poligoni convessi). I poligoni concavi usano un tessellator

Fragment Processing

Processa il colore come affine combination del valore dei tre triangoli

Z-Buffer / Visibility

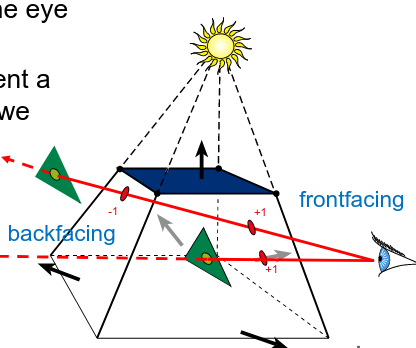
Culling → nascondi quel che non vedi di un oggetto coperto dallo stesso oggetto Calcoliamo la backface culling con il coseno della normale (se positivo)

Hidden surface Removal (HSR) → nascondo parti di poligoni nascoste da altri oggetti 2 approcci per questo in base al sistema coordinate Object space (VCS) → for each triangle, for each pixel Image space (SCS) → for each pixel, for each object

Painter’s algorithm → disegna partendo da dietro, override dove capita

• Depth sort → non funziona per alcuni casi particolari Ray casting → raggio che guarda la prima intersezione e si ricorda l’oggetto per quel pixel Z-Buffer Algorithm → it’s like “painting over” a pixel if something closer comes up (it’s easy to implement and lightweight, the standard)

2.2 Lighting and shading

Gli oggetti che riflettono la luce sono Opachi → la luce incidente e’ riflessa o assorbita Traslucidi → trasmissione della luce significante (specchi)

I modelli di luce possono essere

• Basati su fisica (rendering equation)
• Empirici → approssimazione, seguiamo i raggi di luce che arrivano all’osservatore direttamente e tramite riflessi

Il colore in un punto e’ definito attraverso le fonti di luce, le proprieta’ riflettenti del materiale e il modello d’illuminazione

• Modello locale → semplice, importa solo la luce diretta dalla fonte
• Modello globale → conta anche la luce indiretta

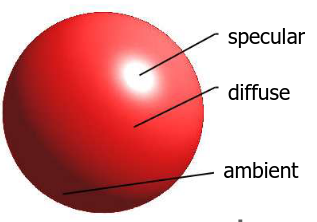
Il materiale puo’ riflettere la luce in 3 modi, gestiti singolarmente 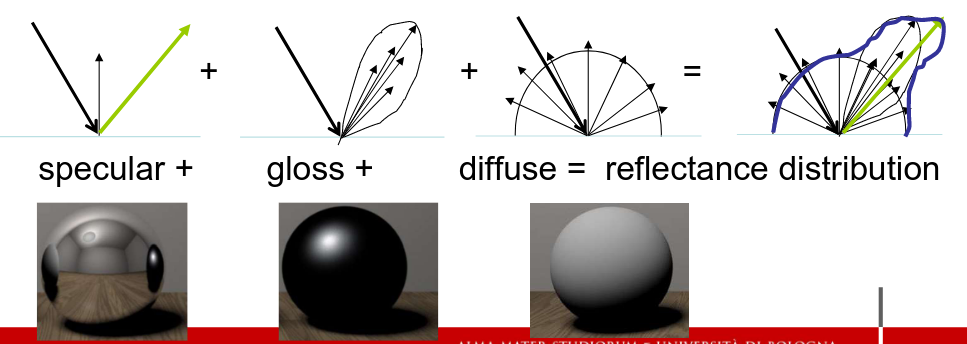Un materiale ha queste proprieta’ $K_{a,d,s,e}\in [0,1]$

• $k_a$ → ambient
• $k_d$ → diffuse reflection coefficient
• $k_S$ → specular reflection coefficient
• $k_e$ → emissive (self emission of light) $n_s$ → specular reflection exponent Il modo in cui un materiale riflette la luce e’ riferito come Reflection model

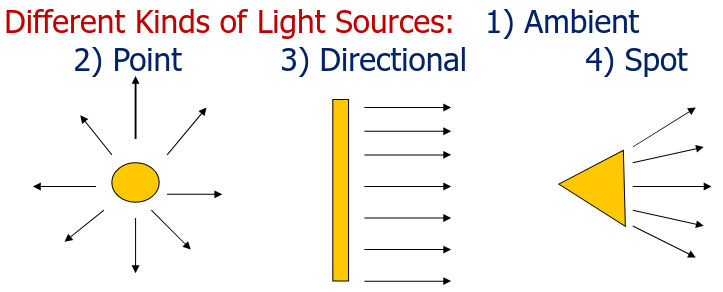
La luce puo’ essere generata in 4 modi

Phong’s local illumination model $I_{\lambda }=k_e+I_a{k}_a+I_d{k}_d+I_S{k}_S$

• $I_a$ → ambient intensity
• $I_d$ → diffusion intensity, $I_l\max (0,l\ast n)$ where $I_l=$Source light intensity, $l$ and $n$ from Lambert’s cosine law
• $I_S$ → reflection intensity In sostanza, moltiplica le proprieta’ del materiale alle intensita’ corrispettive per poi sommarle

Lambert’s cosine law → la luce in ogni unita’ e’ proporzionale all’angolo tra la fonte di luce e l’orientazione della superficie

Attenuation term → la luce si attenua dopo una certa distanza, lo prendiamo in considerazione

Blinn-Phong Lighting Model → usiamo un halfway vector $h$ invece del dot product che usiamo nel modello Phong

Shading per frammenti→ assegnare il colore al pixel Dal flat shading, possiamo

• Calcolare Phong ad ogni pixel
• Calcolare normali di ogni vertice per approssimare la superficie che rappresentano

Gouraud Shading

• Normale computata ai vertici, colore deciso in base alla normale e phong
• intesita’ colore = barycentric interpolation delle intensita’ ai vertici
• una lighting evaluation per vertex
• manca highlight/spotlight e soffre il banding effect (discontinuità nel modello causa bug nella colorazione)

Phong shading

• Normale computata ad ogni vertice, poi interpolati sulla faccia
• Colore pixel = appliga phong light ad ogni pixel della faccia usando il vettore normale interpolato
• una lighting evaluation per pixel
• Computationally expensive

2.3 Shadows & Transparency

Dobbiamo simulare ombra e penombra Per la penombra blurriamo l’ombra nello spazio immagine, non accurato ma cheap

Ombre generate

1. Ombra su superfici piane → cast la forma dell’oggetto sul piano
2. Shadow map algorithm → stesso metodo del nascondere superfici nascoste ma applicato alle fonti di luce ed usa lo z-buffer per ricavare i punti in ombra
   • Shadow Depth Maps → la computazione viene salvata in una texture chiamata shadow map ed usata successivamente
   • Light maps → Crea shadow maps dalle silhouette degli oggetti dalla fonte di luce e poi la proietta
3. Shadow volumes → rappresento un volume di spazio delle zone in ombra e traccio una line dal POV, se intercetto un volume il punto e’ in ombra
   • 

Ambient Occlusion → simulazione ombre dagli oggetti che bloccano la luce ambientale (anche nello stesso oggetto)

1. Ray casting → lancio raggi in ogni direzione da un punto di un oggetto, raggio non bloccato = aggiunge luce
2. Screen Space Ambient Occlusion (SSAO) → Il fragment shader computa i depth values intorno al pixel e cerca di capire quanto e’ oscurato il pixel

Renderizzare trasparenza → Alpha channel definisce l’opacita’ dell’oggetto

• Le superfici opache vanno renderizzate prima delle trasparenti (altrimenti il colore finale del pixel sara’ sbagliato)

Order-Independent Transparency OIT → sort dei pixel fatto nel fragment shader che rispetti quanto scritto sopra Algoritmo idea nelle slide

• Keep a list of colors for each pixel,
• sort them by depth,
• blend them together in the fragment shader.

2.4 Texture Mapping

Texturing → applica immagini/pattern a oggetti geometrici

• 2D mapping → Come vernice sull’oggetto
• 3D mapping → Come pattern intrinseco nell’oggetto (eg. legno, quarzo) Texel → pixel in una texture Parameterization → mappare su un piano 2D una superficie 3D, si puo’ fare anche in patches per oggetti complessi

in rasterization i vertici hanno mapping, l’interno viene interpolato

2 step nel mapping

• S mapping → superfice intermediaria semplice
• O mapping → wrap della S map sull’oggetto

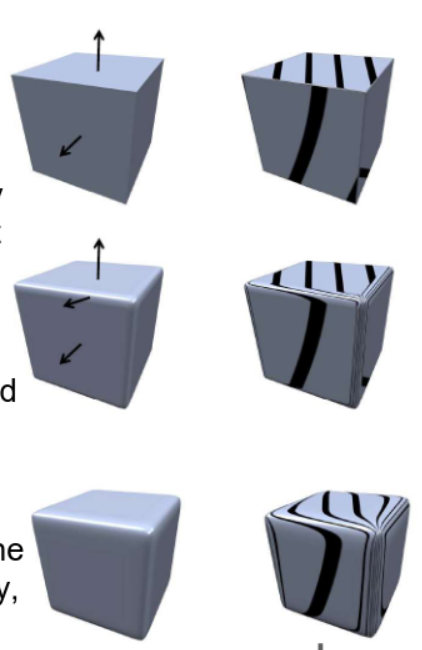
Bump map → height map che definisce un displacement non geometrico sull’oggetto, salvo in grayscale, seguo la normale del punto nell’oggetto Normal map → Modifico le normali, salvo in RGB per indicare coordinate XYZ del vettore direzione

Displacement mapping → displacement geometrici sulla mesh, la complica

Procedural texturing → 3D textures generate con Noise visto a computer vision (eg. Perilin), genera pattern interessanti che danno coerenza spaziale alla texture

Environment mapping → gestisce i riflessi tipo gli specchi negli oggetti. Creiamo una Env-map dell’area circostante e la mettiamo come texture all’oggetto

Sampling, Texture Filtering Texture e grandezza di un pixel a schermo variano, come gestiamo i diversi casi?

• Magnification → il Texel e’ piu’ grande del pixel
  • Interpoliamo (nearest neighbor/ bi or tri -linear interpolation)
• Minification → il Texel e’ piu’ piccolo del pixel
  • Mipmaps, copie scalate delle texture preprocessate
  • Usiamo un fettore scalare dato dal rapporto texel/pixel

Aliasing effect → “jaggies”, quando un oggetto sembra pixellato brutto Tecniche anti-aliasing

• SuperSampling AA → render at higher res, blur, resample at lower res
• Multisample Anti-Aliasing (MSAA) → render multiple samples per pixel on edges and average the results
• Prefilter texture map
• Fast Approximate Anti-Aliasing (FXAA) → post-processing technique that Blurs entire image slightly (low cost in shader)

Physical Based Rendering PBR materials → Materiale realistico, utilizza molte mappe sovrapposte

• Albedo
• Normal
• Gloss (or Roughness)
• Metalness/Specular
• Displacement/Height
• Ambient Occlusion
• Refraction
• Emissive/Glow

Refraction Map → mappa per rifrazione della luce come passa attraverso un oggetto Emissive Map → Illuminazione dell’oggetto stesso

2.5 Ray tracing

Diversi modi per gestire il ray tracing, di base si calcola come Output Luce = Luce emessa + Luce riflessa

Bidirectional Reflectance Distribution Function (BRDF) → gestisce quanto e come una luce e’ riflessa, seguendo

• Specular term (effetto specchio)
• Diffuse term (effetto “scattered”)

L’algoritmo base funziona in backmap: casta un numero di raggi dallo spettatore verso l’oggetto fino alla fonte di luce

1. genera raggio primario
2. trova oggetto piu’ vicino che appartiene al raggio
3. ray casting (simula illuminazione dal punto trovato)

Pipeline

• Shadow/Direct Illumination (Ray Casting)
  • Shadow ray → ray from surface to all light sources, if it intersects another object do not count the light source
• Reflection
  • Reflection ray → start from point of intersection (eye ray to reflective point) and send a ray toward specular reflection, keep bouncing until light source or out of frame
• Refraction
  • Transmission ray → ray passes trough transparent object, changes direction of ray
  • The amount of refraction is calculated using the index of refractions.
• Recursive Ray Tracing
  • Da un raggio generato, ricorsivamente genera raggi di reflection e transmission fino ad una depth definita

La RTX aggiunge soft shadows facendo partire piu’ raggi da un singolo bounce

Capire l’intersezione su una superficie e’ computazionalmente costoso

Path Tracing → algoritmo di approssimazione ray tracing, casta un raggio casuale ad un bounce e approssima i colori con i risultati adiacenti

3 - Animation

3.1 Object/Camera path

Muovere un’entita’ attraverso un percorso (path)

Path = keyframe di un posto + interpolazione tra keyframes

Modello fisico per descrivere un path → particella che si muove in tempo $u$, che definisce

• Posizione in base ad u
• Vettore velocita’ $V$ in base ad u
• Speed (magnitude vettore velocita’), norma 2 di $V$

Arc-length parameterization → distanza percorsa in un tempo determinato $u$ dal punto di partenza (si trova con un integrale) Chord-length → approssimazione discretizzata dell’arc length con una linea poligonale, $u$ visto tra 0 ed 1, e’ facile controllare la velocita’ dalla chord-length

Speed control function $d(t)$ → definisce il punto dove l’entita’ si trova ad ogni $t$, diversi andamenti (regolare, stazionario etc., plot distanza e tempo)

Orientation control

FRENET Frame along a path, vuol dire che definiamo l’orientazione dell’entita’ come proprieta’ nel percorso Le proprieta’ sono le stesse che troviamo nella camera nella rendering pipeline

• Local right coordinate frame $(u,v,w,P(s))$
  • w → direction
  • v → up-vector (where up is)
  • u → points left
  • P(s) → path

center of interest (COI) → rimani a fissare un punto preciso

• $w=COI-POS$ (POS = observer position)
• $u=w\times y-axis$
• $v=u\times w$ Possiamo creare diversi punti di interesse che formano un secondo path che definisce dove guarderemo “Look ahead” →Possiamo guardare avanti nello stesso path (stratagemma per seguire oggetti)

3.2 Animation

Articulated figure → parti rigide chiamate Bones connesse da Joints, rappresentato da un tree, ogni nodo e’ un osso, gli archi sono i joints

Rigging → costruire i controlli del modello 3D (scheletro, joints)

3 tipi di animazioni

• Basati su fisica/procedurali
  • particelle (sistemi di particelle), cose complesse simulabili (vestiti, pelo)
  • Focus sulle forze che agiscono sulle simulazioni (interne ed esterne)
• Data driven, aka Motion capture
  • Pipeline
    • Calibration
    • Capture
    • 3D reconstruction
    • Fitting to the skeleton
    • Post-Processing
• Keyframing
  • Definibile con direct ed inverse kinematics
    • 
  • Interpolazione della rotazione tricky, vengono usati i quaternioni con Slerping, mentre la rappresentazione delle rotazioni all’utente con gli angoli di Eulero (si converte ogni volta che bisogna interpolare tra quaternioni e angoli di Eulero) Skinning → relaziona scheletro rigged e poligoni della mesh

Linear blend skinning → tecnica che assegna ad ogni vertex piu’ ossa, per gestire bene la mesh intorno